[Spoj GSS3]Can you answer these queries III

发表于 | 分类于 ， | | 阅读次数:

题目

题目描述

给定长度为N的数列A，以及M条指令 (N≤500000, M≤100000)，每条指令可能是以下两种之一：
“2 x y”，把 A[x] 改成 y。
“1 x y”，查询区间 [x,y] 中的最大连续子段和，即 max(x≤l≤r≤y)⁡ { ∑(i=l~r) A[i] }。
对于每个询问，输出一个整数表示答案。

输入

第一行两个整数N,M

第二行N个整数Ai

接下来M行每行3个整数k,x,y，k=1表示查询（此时如果x>y，请交换x,y），k=2表示修改

输出

对于每个询问输出一个整数表示答案。

样例输入

1
2
3
4
5
5 3
1 2 -3 4 5
1 2 3
2 2 -1
1 3 2

样例输出

1
2
2
-1

提示

数据范围与约定

对于100%的数据: N≤500000, M≤100000, |Ai|<=1000

题解

树存储空间大小

这道题与原题略微有点区别，数据输入顺序不一样，以及范围更大了，但是稍微改一下就可以过了。
第一个问题，为什么树要开到4*N？
首先，我们构造的线段树有可能是完全二叉树（最好情况），叶子节点存储的就是我们每一个点的数据，而我们可以分析下完全二叉树的图。

不难发现，我们设节点有n个，那么二叉树的层数为$ log_2(n+1) $
而设叶子节点有k个，那么就得到一个k与n的关系：$ k(1-(1/2)^n)=2n $
n随k的变化关系曲线为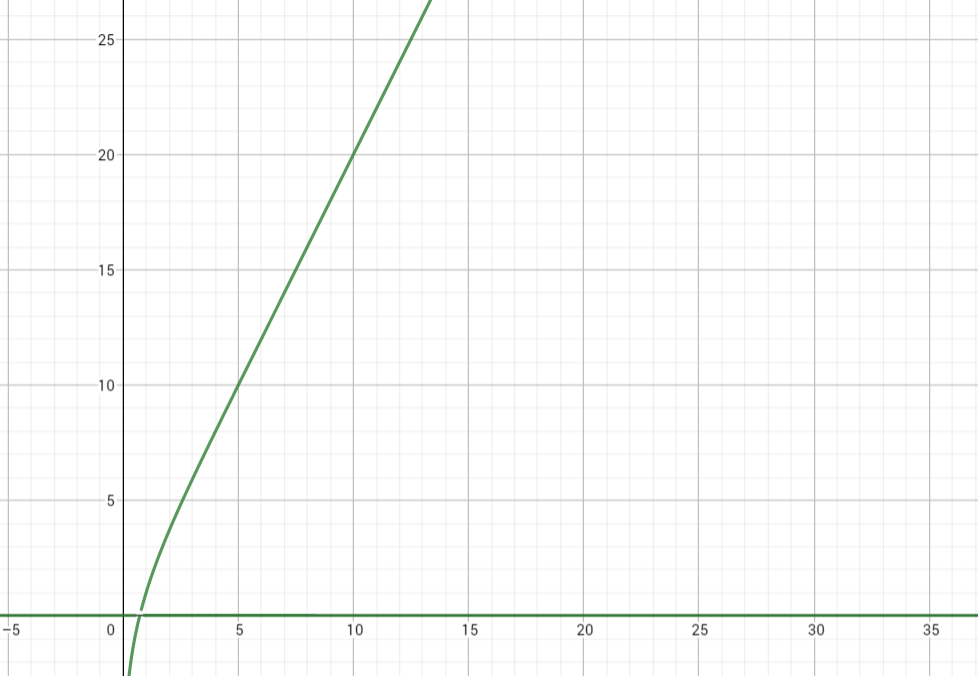

当k趋于无穷大，$ n=2k $

而对于最坏情况，请参见这篇文章
对于最坏的情况我们要开4n的空间来存储。

树存储方式

第二个问题，我们要存树，这里可以开一个结构体，里面有四个变量
| 变量名称 | 变量作用 |
|-|:-:|-|
| data | 储存该区间内的最大连续子段和 |
| ldata | 储存该区间从左端开始的最大和 |
| rdata | 储存该区间从右端开始的最大和 |
| sum | 储存该区间内的所有数的和 |
这些就够了，不必纪录左子树和右子树。

建树

对于每个叶子节点（r==l），我们给他们赋值，而其他节点我们就需要来分析情况了。

sum的值

sum的值还用说吗，就是左子树的sum+右子树的sum

data的值

data是该区间内的最大连续子段和，所以对于data就有几种可能，而我们要做的就是取最大的：
1.data=左子树data
2.data=右子树data
3.data=左子树rdata+右子树ldata

ldata和rdata的值

ldata储存该区间从左端开始的最大和，所以：
1.ldata=左子树ldata
2.ldata=左子树sum+右子树rdata
rdata同理

改变值

改变值其实就是建树，只不过因为只改变一个值，所以分治时要么是左子树，要么是右子树，改变完后要注意重新维护其他点的值。

查询值

查询值较为复杂，但我们也可以把它看成一个建树的过程。
首先，对于我们要查询的范围，如果这个范围大于等于我们分治下去的范围，那么就返回这个范围的值。（实际上就是我们建树时存在这个范围的点）
如果这个范围没有点满足，那么我们可以用叶子节点建树来建成我们想要的范围的点。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define MAXN 500000
struct Ttree{
	int data;
	int ldata,rdata;
	int sum; 
}t[MAXN*4],tmp0;
int n,m;

void push_up(int l,int r,int k){
	t[k].sum=t[k*2].sum+t[k*2+1].sum;
	t[k].data=max(t[k*2].data,t[k*2+1].data);
	t[k].data=max(t[k*2].rdata+t[k*2+1].ldata,t[k].data);
	t[k].ldata=max(t[k*2].ldata,t[k*2].sum+t[k*2+1].ldata);
	t[k].rdata=max(t[k*2+1].rdata,t[k*2+1].sum+t[k*2].rdata);
	return;
}

void make(int l,int r,int k){
	if(l==r){
		scanf("%d",&t[k].data);
		t[k].ldata=t[k].rdata=t[k].sum=t[k].data;
		return;
	}
	int mid=(l+r)/2;
	make(l,mid,k*2);
	make(mid+1,r,k*2+1);
	push_up(l,r,k);
	return;
}

Ttree ask(int L,int R,int l,int r,int k){
	if(L<=l&&r<=R)return t[k];
	int mid=(l+r)/2;
	Ttree res1;
	if(L<=mid)res1=ask(L,R,l,mid,k*2);
	else res1=tmp0;/*目前分治的点的左子树不包含要查询的左端范围，不参与建树，tmp0初始化很小，在取最大值的时候含有它的情况会被忽略掉，但是tmp0.sum初始化还是0*/
	Ttree res2;
	if(R>mid)res2=ask(L,R,mid+1,r,k*2+1);
	else res2=tmp0;//同理
	Ttree res={0};
	res.sum=res1.sum+res2.sum;
	res.data=max(res1.data,res2.data);
	res.data=max(res1.rdata+res2.ldata,res.data);
	res.ldata=max(res1.ldata,res1.sum+res2.ldata);
	res.rdata=max(res2.rdata,res2.sum+res1.rdata);
	return res;
}

void change(int x,int y,int l,int r,int k){
	if(l==r){
		t[k].data=y;
		t[k].ldata=t[k].rdata=t[k].sum=t[k].data;
		return;
	}
	int mid=(r+l)/2;
	if(x<=mid)change(x,y,l,mid,k*2);
	else change(x,y,mid+1,r,k*2+1);
	push_up(l,r,k);
	return;
}

int main(){
	tmp0.data=tmp0.ldata=tmp0.rdata=-1e9;
	scanf("%d%d",&n,&m);
	make(1,n,1);
	for(int i=1;i<=m;i++){
		int k,x,y;
		scanf("%d%d%d",&k,&x,&y);
		if(k==1){
			if(x>y)swap(x,y);
			printf("%d\n",ask(x,y,1,n,1).data);
		}else{
			change(x,y,1,n,1);
		}
	}
	return 0;
}